1 假设两个链表都没有环

解题思路

a. 直接循环判断第一个链表的每个节点是否在第二个链表中。但，这种方法的时间复杂度为O(Length(h1) * Length(h2))。显然，我们得找到一种更为有效的方法，至少不能是O（N^2）的复杂度。

b. 针对第一个链表直接构造hash表，然后查询hash表，判断第二个链表的每个节点是否在hash表出现，如果所有的第二个链表的节点都能在hash表中找到，即说明第二个链表与第一个链表有相同的节点。时间复杂度为为线性：O(Length(h1) + Length(h2))，同时为了存储第一个链表的所有节点，空间复杂度为O(Length(h1))。是否还有更好的方法呢，既能够以线性时间复杂度解决问题，又能减少存储空间？

 

c.转换为环的问题。把第二个链表接在第一个链表后面，如果得到的链表有环，则说明两个链表相交。如何判断有环的问题上面已经讨论过了，但这里有更简单的方法。因为如果有环，则第二个链表的表头一定也在环上，即第二个链表会构成一个循环链表，我们只需要遍历第二个链表，看是否会回到起始点就可以判断出来。这个方法的时间复杂度是线性的，空间是常数。

 

d.进一步考虑“如果两个没有环的链表相交于某一节点，那么在这个节点之后的所有节点都是两个链表共有的”这个特点，我们可以知道，如果它们相交，则最后一个节点一定是共有的。而我们很容易能得到链表的最后一个节点，所以这成了我们简化解法的一个主要突破口。那么，我们只要判断两个链表的尾指针是否相等。相等，则链表相交；否则，链表不相交。

所以，先遍历第一个链表，记住最后一个节点。然后遍历第二个链表，到最后一个节点时和第一个链表的最后一个节点做比较，如果相同，则相交，否则，不相交。这样我们就得到了一个时间复杂度，它为O((Length(h1) + Length(h2))，而且只用了一个额外的指针来存储最后一个节点。这个方法时间复杂度为线性O(N)，空间复杂度为O(1)，显然比解法三更胜一筹

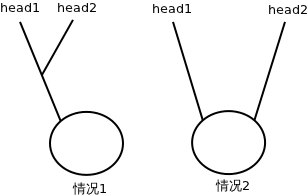
2 假设两个链表都有环，情况只有2种：相交于”环上”或相交于”不是环的部分”。因此环一定是在公共部分上的。假如知道其中一个链表上环的任意一个节点，则只需要判断是否在另一个链表上就行了。这里有个疑问？一般意义上，链表有环并不存在这种形式：1->2->3->2->4?

//判断带环不带环时链表是否相交  //2.如果都不带环，就判断尾节点是否相等  //3.如果都带环，判断一链表上俩指针相遇的那个节点，在不在另一条链表上。  bool detect(Node * head1, Node * head2)  {      Node * circleNode1;      Node * circleNode2;      Node * lastNode1;      Node * lastNode2;            bool isCircle1 = isCircle(head1,circleNode1, lastNode1);      bool isCircle2 = isCircle(head2,circleNode2, lastNode2);            //一个有环，一个无环      if(isCircle1 != isCircle2)          return false;      //两个都无环，判断最后一个节点是否相等      else if(!isCircle1 && !isCircle2)      {          return lastNode1 == lastNode2;      }      //两个都有环，判断环里的节点是否能到达另一个链表环里的节点      else      {          Node * temp = circleNode1->next;  //updated，多谢苍狼 and hyy。          while(temp != circleNode1)            {              if(temp == circleNode2)                  return true;              temp = temp->next;          }          return false;      }            return false;  }

3   求相交的第一个元素

对于1中相交，只要知道两个链表长度L1和L2，那么让长的那个先走abs(L1-L2),然后一起走，相同的那个节点就是第一个元素

//求两链表相交的第一个公共节点Node* findIntersectNode(Node *h1,Node *h2){    int len1 = listLength(h1);          //求链表长度    int len2 = listLength(h2);    //对齐两个链表    if(len1 > len2)    {        for(int i=0;i
     
      next;    }    else     {        for(int i=0;i
      
       next;    }    while(h1 != NULL)    {        if(h1 == h2)            return h1;        h1 = h1->next;        h2 = h2->next;        }    return NULL;}
      
     

http://wuchong.me/blog/2014/03/25/interview-link-questions/

http://blog.csdn.net/v_july_v/article/details/6447013